In this tutorial, we’ll be creating our own Bitcoin addresses in Ruby. The easy way uses the bitcoin-ruby gem, but this doesn’t teach us much; so we’ll do it ourselves using only basic hashing and an elliptic curve cryptography libraries.

require 'bitcoin'
key = Bitcoin::generate_key
address = Bitcoin::pubkey_to_address(key[1])
# address => 16aqnGNe8GXKajL6Hjj6fGpPBqve8QnNfd

Introduction

Some high level notes:

  • We have 3 main components:

    1. Private keys
      • Lets you sign new transactions, thereby spending your bitcoins.
      • 256 random bits
    2. Public Keys
      • Proves that you own bitcoins associated with a certain address
      • An elliptic curve public key of the above private key
    3. Public Address
      • Give this to people, so that they can send you bitcoins.
      • Hash of the public key

  • The private key deterministically generates the public key, which deterministically generates the public address (the same private key will always generate the same public key and public address).

  • These “generation” functions involve one-way functions (once you perform the function, you can’t go back and determine the inputs). It’s practically impossible to get the public key from a public address, or a private key from a public key.

  • Compressed public keys are now widely used amongst the most popular bitcoin software. The public address of a compressed public key is different than the public address of the uncompressed public key.

Disclaimer: I am not a cryptographer, this is for academic experimentation only.

I’ve used some helper functions for common conversions (hex converters, string converters, base58 encoding). This utility file can be downloaded here.

Private Key:

Step 1. Generate 256 random bits.

You can get this from /dev/urandom, flip a coin 256 times, roll a 16-sided dice 64 times, point a webcam at your lavalamp, etc, but here, we’ll just take a hash of a simple phrase. Bear in mind that the elliptic curve is defined over a prime field, so our private key must be less than our chosen prime.

Note: Did I mention that this implementation should only be accepted as academic experimentation? Scammers have already generate addresses based on common words/phrases and steal any bitcoins that get sent to those addresses.

require digest
passphrase = "bitcoins are cool"
priv_key = Digest::SHA256.digest(passphrase)
p = 2**256 - 2**32 - 2**9 - 2**8 - 2**7 - 2**6 - 2**4 - 1
if priv_key.to_bignum > p
  raise "Private key invalid" 
end
# priv_key.to_hex => 9e524de478970a9621c0e52890805d5f28e3620892ba6bfa701b026c6ee10a52

Just to be clear, the private key can be exressed in multiple ways:

  • Binary: 1001111001010010010011011110010001111000100101110000101010010110001000011100000011100101001010001001000010000000010111010101111100101000111000110110001000001000100100101011101001101011111110100111000000011011000000100110110001101110111000010000101001010010
  • Integer: 71610849129504069670807627525562295685404995395280754758942009276479161043538
  • Hex: 9e524de478970a9621c0e52890805d5f28e3620892ba6bfa701b026c6ee10a52

These are merely different representations of the same thing, and are all equivalent. As we proceed, we’ll need to jump around different representations depending on what we’re doing. Don’t be alarmed.

We could actually stop here. These 256 random bits ARE your private key, but if you want to use this key with any mainstream bitcoin application, the private key must be in wallet import format (WIF format). To do that:

Step 2. Prepend version, append compression flag

The version number depends on the network.

  • Bitcoin = 0x80
  • Testnet = 0xEF (Testnet is a “bitcoin playground” where developers can test their applications against a live, bitcoin-like network where coins have no value)

Compression Flag = 0x01

Note: Compression flag is needed to make private keys completely deterministic. As stated above, compressed and uncompressed public keys generate different public addresses. The compression flag signals which of those addresses this private key should generate.

# Note: adding the "b" makes a binary representation of our byte before concatenating, to avoid encoding issues
priv_key_and_version = "\x80".b + priv_key + "\x01".b
# priv_key_and_version.to_hex => 809e524de478970a9621c0e52890805d5f28e3620892ba6bfa701b026c6ee10a5201
Step 3. Add checksum

Checksum is the first 4 bytes of the double sha256 hash of our input. It is used to ensure that every bit is correct; if a single bit is off (mistyped), we will know about it.

def cat_checksum (input)
  firstSHA  = Digest::SHA256.digest(input)
  secondSHA = Digest::SHA256.digest(firstSHA)
  input + secondSHA[0,4]
end

priv_key_and_version_and_checksum = cat_checksum(priv_key_and_version)
# priv_key_and_version_and_checksum.to_hex => 809e524de478970a9621c0e52890805d5f28e3620892ba6bfa701b026c6ee10a520140d9c9e7
Step 4. Base58 Encoding

We currently have 38 bytes of data. Using the digits 0-9. we can express this data as a 92 digit long integer. Using hex (16 possible characters) we express this in 76 characters (as shown above). If we use 58 possible characters, the data can be expressed in only 52 characters. The characters used for Base58 are:

  • 1-9 (9)

  • a-z except ‘l’ (25)

  • A-Z except ‘I’,’O’ (24)

privateWIF = priv_key_and_version_and_checksum.to_base58
# privateWIF => L2XU3tBMCgmAb16LRcrPenccYdUCGKgahkW1oZ4diHuk3dvb6WDL

I’ve included the bitcoin-ruby base58 encoder here.

Public Key

Step 5. Evaluate:

This is where Elliptic Curve Cryptography comes in. I’ll go into how this all works in a later post, but for now, we’ll simply use this equation.

= 77 digit long integer that we generated in step 1.

G = the “generator point”, a special point on the elliptic curve

  • It has x coordinate: 55066263022277343669578718895168534326250603453777594175500187360389116729240
  • and y coordinate: 32670510020758816978083085130507043184471273380659243275938904335757337482424

When we multiply the generator point with our private key, we get a new point on the elliptic curve. The x and y cooordinates of this point act as our public key. Because you can’t easily divide points on an elliptic curve, it’s computationally impractical to generate the private key given our knowledge of the public key and the generator point.

Note: Bitcoin uses the “secp256k1” curve, which defines it’s own generator point. Every application which uses the secp256k1 curve uses the same generator point.

curve = ECDSA::Group::Secp256k1
pub_key = curve.generator.multiply_by_scalar(priv_key.to_bignum)
# pub_key.x => 107755497148048731412938604358975700840069163823903109146820905484112739528923
# pub_key.y => 24245920055987556528993042428760322520988269343242132634556250883291122420691

Note: We’re using the “ecdsa gem” because the OpenSSL library is poorly documented and confusing. Explanation here.

Step 6. Compress

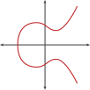
Because elliptic curves are symmetric about the x axis; given any x coordinate, there exist only 2 possibilities for the y coordinate. Uncompressed public keys include the full y coordinate (a really big number), but we can save space on the blockchain by indicating which of the 2 possible y-coordinates we use.

If the y coordinate is even, public keys have the form:

  • 0x02 + x coordinate

If y coordinate is odd:

  • 0x03 + x coordinate
# pub.x is a Bignum, so we must concatenate our compression byte with the hex representation of pub_key.x
if pub_key_point.y % 2 == 0 # y is even
  leader = "\x02"
else
  leader = "\x03"
end
pub_key = leader + [pub_key_point.x.to_hex].pack("H*")
# pub_key.to_hex => 03ee3b7337eb52d1e8bd7ee271db9aa43a67750ff483870ab2753d2e13922970db

Why must the 2 y coordinates have unique parity? Because the elliptic curve is over a prime finite field, when we change sign, we flip parity. Illustrated simply, 5 modulus 7 = 5 is odd, but -5 modulus 7 = 2, which is even.

We now have our public key.

Public Address

Step 7. Hash public key

Next, we hash the public key. This compresses our key from 256 bits to 160 bits.

pub_key_sha256 = Digest::SHA256.digest(pub_key_with_lead)
pub_key_hash = Digest::RMD160.digest(pub_key_sha256)
# pub_key_hash.to_hex => 5355f7bb58765e07a20f978b6e2437e99a5e92d3
Step 8. Prepend version, append checksum

The version number depends on the network, and is different than the version used in step 2.

  • Bitcoin = 0x00
  • Testnet = 0x6F

Checksum is computed the same way it was in step 3.

pub_key_hash_and_version_and_checksum = cat_checksum("\x00" + pub_key_hash) 
# pub_key_hash_and_version_and_checksum.to_hex => 005355f7bb58765e07a20f978b6e2437e99a5e92d3f612577e
Step 9. Base58 Encode.
pub_addr = pub_key_hash_and_version_and_checksum.to_base58 
# pub_addr => 18be54dbyAth7CR4ymeoQBpzwinLW5Qe1K

We can now share this address with our friends, convert it to a QR code, get it tatooed on our bodies, and watch the bitcoins rush in.

– rf

===

Download the code here.

References/Additional Reading